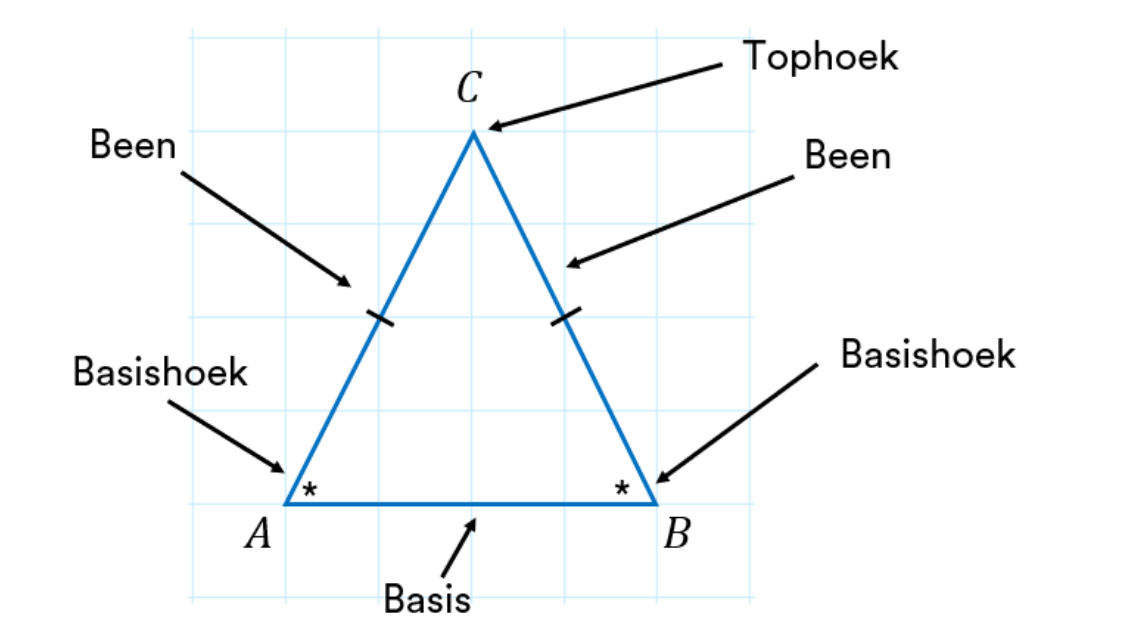
Ooit gefascineerd geweest door de symmetrie van een gelijkbenige driehoek? Deze driehoeken, met hun twee gelijke zijden en twee gelijke hoeken, zijn niet alleen visueel aantrekkelijk, maar ook fundamenteel in de geometrie. Maar wat is nu precies de som van de hoeken in een gelijkbenige driehoek? Laten we dieper duiken in deze intrigerende wereld van hoeken en zijden.
De som van de hoeken in elke driehoek, inclusief een gelijkbenige driehoek, is altijd 180 graden. Dit is een fundamenteel principe in de Euclidische meetkunde. Deze kennis opent de deur naar het berekenen van onbekende hoeken in een gelijkbenige driehoek, mits we ten minste één hoek kennen.
Het begrijpen van de hoeken van een gelijkbenige driehoek is cruciaal voor diverse toepassingen, van architectuur en engineering tot kunst en design. Stel je voor dat je een dak wilt ontwerpen met een gelijkbenige driehoekige vorm. Kennis van de hoeken is essentieel voor de stabiliteit en esthetiek van het ontwerp.
De geschiedenis van de gelijkbenige driehoek gaat terug tot de oude Grieken, met wiskundigen zoals Euclides die de eigenschappen ervan vastlegden in zijn beroemde werk 'Elementen'. Deze kennis vormde de basis voor verdere ontwikkelingen in de geometrie en trigonometrie.
Een gelijkbenige driehoek wordt gedefinieerd als een driehoek met twee gelijke zijden. Deze gelijke zijden staan tegenover gelijke hoeken, wat een belangrijk kenmerk is bij het oplossen van problemen met betrekking tot gelijkbenige driehoeken. Bijvoorbeeld, als de tophoek van een gelijkbenige driehoek 50 graden is, dan zijn de twee basishoeken elk (180 - 50) / 2 = 65 graden.
Voordelen van het begrijpen van de hoekenom van gelijkbenige driehoeken:
1. Probleemoplossing: Je kunt onbekende hoeken berekenen in complexe geometrische figuren die gelijkbenige driehoeken bevatten.
2. Ontwerp en constructie: Kennis van de hoeken is essentieel voor het ontwerpen van stabiele en esthetisch aantrekkelijke structuren.
3. Begrip van wiskundige concepten: Het vormt een basis voor het leren van meer geavanceerde geometrische en trigonometrische concepten.
Veelgestelde vragen:
1. Wat is de som van de hoeken in een gelijkbenige driehoek? 180 graden.
2. Hoe bereken ik de basishoeken als ik de tophoek weet? Trek de tophoek af van 180 graden en deel het resultaat door 2.
3. Wat is een gelijkbenige driehoek? Een driehoek met twee gelijke zijden en twee gelijke hoeken.
4. Waar worden gelijkbenige driehoeken gebruikt? In architectuur, engineering, kunst, design, en meer.
5. Wat is de relatie tussen de zijden en hoeken van een gelijkbenige driehoek? De gelijke zijden staan tegenover de gelijke hoeken.
6. Kan een gelijkbenige driehoek ook rechthoekig zijn? Ja, als een van de hoeken 90 graden is.
7. Wat is de geschiedenis van de gelijkbenige driehoek? De studie van gelijkbenige driehoeken gaat terug tot de oude Griekse wiskunde.
8. Hoe kan ik meer leren over gelijkbenige driehoeken? Door middel van online bronnen, wiskundeboeken en educatieve apps.
Tips en trucs: Teken altijd een schets van de driehoek en label de bekende hoeken en zijden om het probleemoplossingsproces te vereenvoudigen. Onthoud de basisformule: de som van de hoeken in een driehoek is 180 graden.
Conclusie: Het begrijpen van de hoeken van een gelijkbenige driehoek is fundamenteel in de geometrie en heeft talloze praktische toepassingen. Van het ontwerpen van gebouwen tot het oplossen van complexe wiskundige problemen, deze kennis is onmisbaar. Door de eigenschappen van gelijkbenige driehoeken te beheersen, open je de deur naar een dieper begrip van de wereld om ons heen. Verder onderzoek naar dit onderwerp kan leiden tot een waardering voor de elegantie en symmetrie van geometrische vormen en hun rol in diverse disciplines. Dus, blijf nieuwsgierig en blijf verkennen, de wereld van de geometrie wacht op je!
Alternatieven voor het woord bord ontdek synoniemen en toepassingen
De juiste term voor waterhoogte vinden
Combineer werk en studie jouw droombaan in de zorg
